Kursinhalte
| Themenblöcke | Inhalte |
|---|---|
| Grundlagen | Aussagenlogik, Mengen, Abbildungen, das Zahlensystem, Gleichungen und Ungleichungen, vollständige Induktion, komplexe Zahlen |
| Elementare Analysis | Funktionen, Folgen, Stetigkeit, Ableitung, Integral, elementare Funktionen |
| Lineare Algebra | Lineare Gleichungssysteme, Ebene und Raum, Vektorräume und Basen, Skalarprodukt, Matrizenaddition und - multiplikation, quadratische Matrizen, Elementarmatrizen, inverse Matrizen |
| Analysis | Charakterisierung der reellen Zahlen, (komplexe) Folgen, Konvergenzkriterien, offene und abgeschlossene Intervalle, Intervallschachtelung, Reihen, Potenzreihen, Stetigkeit, Zwischenwertsatz, Eulersche Zahl, Pi |
| Vertiefung Analysis | Eigenschaften differenzierbarer Funktionen, höhere Ableitungen, Taylor-Polynom und -Reihe, Newtonverfahren, Regel von l'Hospital, Ober- und Untersumme sowie Eigenschaften des Integrals, uneigentliches Integral, Integrationstechniken |
| Vertiefung Lineare Algebra | Matrizenrechnung, Eigenvektoren und Eigenwerte, symmetrische Matrizen, Gram-Schmidt-Verfahren |
| Vertiefung Mehrdimensionale Analysis | Funktionen in mehreren Veränderlichen, offene Mengen, Stetigkeit, Differenzierbarkeit, implizite Funktionen, Satz von der Umkehrfunktion, Lösen elementarer Differenzialgleichungen |
Aus folgender Grafik des Intensivkurses 2021 lässt sich der zeitliche Ablauf ableiten.
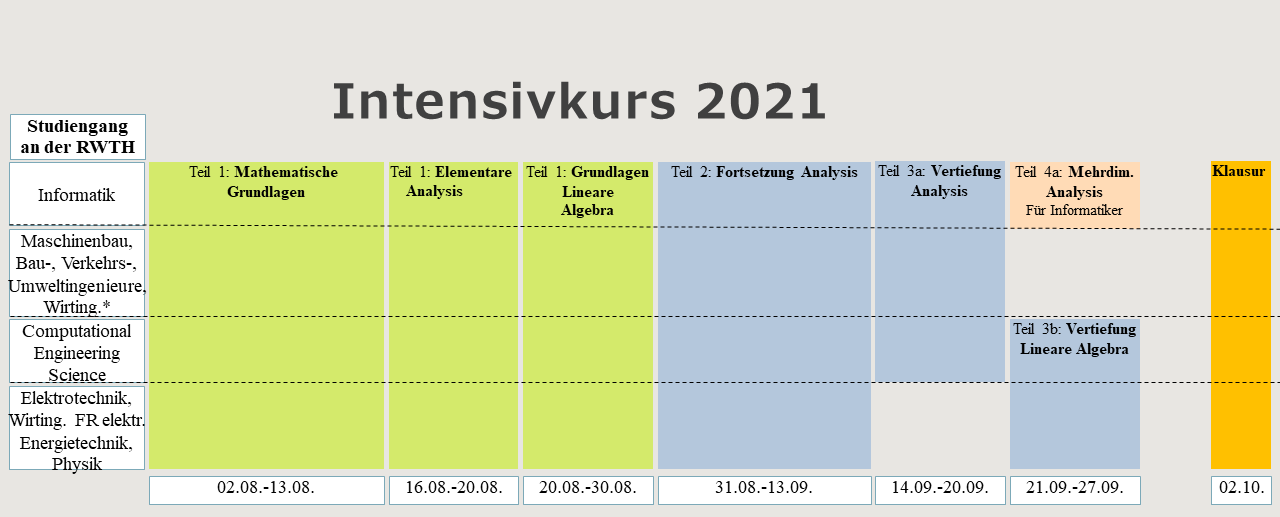
*Wirtschaftsingenieure (an der RWTH) gehören zur Gruppe ihrer entsprechenden Fachrichtung, z.B. "Maschinenbau". Studierende der Geowissenschaften (an der RWTH) können zwischen den Gruppen "Maschinenbau", "CES" und "Physik" frei wählen. Alle weiteren Studiengänge, insbesondere Interessierte anderer beteiligter Hochschulen, wählen ihre Vertiefung entsprechend der Anerkennungsliste.